ちょっと一休みして3Dプログラミングでよく使われれる拡大・縮小、回転、平行移動に関する行列を紹介したいと思います。といっても簡単なことだけです。より複雑な事や正確な説明は数学の解説書にお任せします。
※WebGLでは最終的に立体図形を扱いますが、説明を簡単にするため、ここでは平面図形をベースにして解説していきます。
行列とベクトル
行列
まず行列というのは、1つの行列に複数個の数を割り当てて、
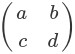
という形で表現したものでした。
そして、この行列に対して、和と積を次のように定義しました。
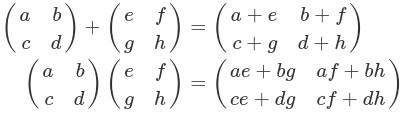
注意が必要な点は積は可換ではないということです。
つまり、
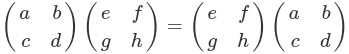
は一般には成ちません。
統合が成立しない例を1つ挙げておきます。
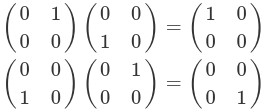
ベクトル
空間(説明の都合上、2次元平面としてください)内の1点は(x,y)の2つの値から成ります。これをベクトルと呼んで、先ほどの行列との積を次のように定義しました。
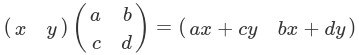
図形の変換
空間内の点を表すベクトルに行列をかけることで、図形の変換を表していきます。
拡大と縮小
(x,y)を原点を中心としてx軸方向にα倍、y方向にβ倍するには、拡大縮小行列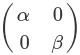 を使います。
を使います。
例えば、x軸方向に2倍に拡大し、y方向に1/2倍に縮小するには、拡大縮小行列を使うと
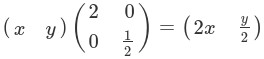
とできます。
回転
(x,y)を原点を中心としてθだけ回転するには、回転行列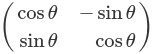 を使います。
を使います。
詳しい説明は省略させてもらいたいと思いますが、高校で習った(もしくは習う)極座標表示を使うと、点(x,y)はある値rとαを使って(r cosα,r sinα)と書き変えることができます。
ですから、点(x,y)をθ回転させるには、
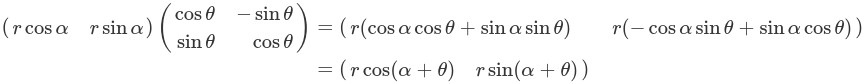
というように回転行列を使って回転できることが分かります。
ちなみに、最後の等号は加法定理を使っています。
※WebGLを使っていく上で数学的なことは直接には使いませんので、雰囲気だけ眺めてもらえればと思います。
平行移動
最後に平行移動を紹介します。一見すると平行移動が一番簡単そうですが、意外と面倒です。
(x,y)をx軸方向にa、y軸方向にbだけ平行移動しようと思うと、
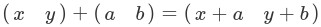
を思い付きますが、これを先ほどまでのように行列との積で表すにはどうすればよいでしょうか?
これまで使ってきた2×2行列ではちょっとできません。
ということで、行と列を1つずつ増やして3×3行列を使うことになります。
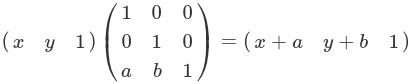
ここで登場する行列が平行移動行列です。
(x,y)の代わりに(x,y,1)が登場し、最後の1が何なのか分かり難いと思います。計算の都合上、最後に1を書くけれど、このベクトルが表す点は(x,y)だと思っておいてください。詳細が気になる人には、参考文献を紹介しておきます。
なお、拡大縮小行列や回転行列も最後に1を追加できます。念のためにここで紹介した行列をまとめてみます。
拡大縮小行列

回転行列
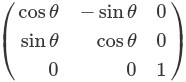
平行移動行列
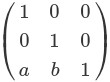
最初に説明しましたが、行列は順序が大切になります。
ここで紹介した行列を使って再度説明すると、「30度回転して、x軸方向に2倍に拡大して、y軸方向に10平行移動する」のと「x軸方向に2倍に拡大して、y軸方向に10平行移動して、30度回転する」のでは最終的には違う図形になります。
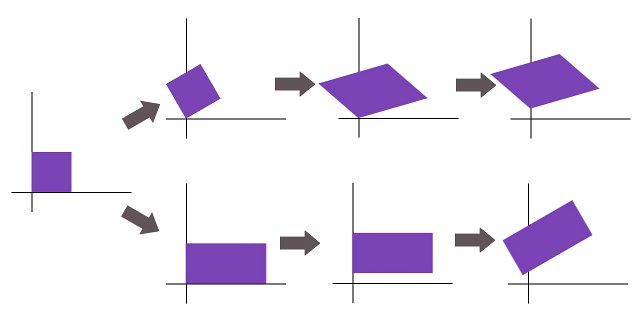
細かなことはWebGLの勉強をしながら少しづつ慣れてみてください。
行列演算ライブラリ
このLessonの最後として、将来のLessonで使う行列演算ライブラリを作成しようと思います。
上で説明した事項をそのままJavaScriptで表現するようにしています。ただし、1点が(x,y)ではなく、(x,y,z)の3点から成りますので、行列も列と行を1つずつ増やして4×4行列になります。
拡大縮小や平行移動は上の説明から簡単に拡張できると思いますが、回転は少し難しいです。「原点の回りに30度回転」とはどういう意味になるか分かりますか?
手元のエンピツを回転しようと思ってもどの方向に回転したらいいのか分かりませんね。ということで、回転は軸を決めて、x軸のまわりに30度回転、y軸のまわりに60度回転、z軸のまわりに90度回転という風に回転することになります。
※回転は他にもいろいろありますがここでは取り上げられませんので、気になる人はいろいろと探してみてください。
function mat4_create()
{
return new Float32Array(16);
}
function mat4_inverse(m1)
{
var m00 = m1[ 0]; m10 = m1[ 1]; m20 = m1[ 2]; m30 = m1[ 3];
var m01 = m1[ 4]; m11 = m1[ 5]; m21 = m1[ 6]; m31 = m1[ 7];
var m02 = m1[ 8]; m12 = m1[ 9]; m22 = m1[10]; m32 = m1[11];
var m03 = m1[12]; m13 = m1[13]; m23 = m1[14]; m33 = m1[15];
var a0 = m00 * m11 - m10 * m01;
var a1 = m00 * m21 - m20 * m01;
var a2 = m00 * m31 - m30 * m01;
var a3 = m10 * m21 - m20 * m11;
var a4 = m10 * m31 - m30 * m11;
var a5 = m20 * m31 - m30 * m21;
var b0 = m02 * m13 - m12 * m03;
var b1 = m02 * m23 - m22 * m03;
var b2 = m02 * m33 - m32 * m03;
var b3 = m12 * m23 - m22 * m13;
var b4 = m12 * m33 - m32 * m13;
var b5 = m22 * m33 - m32 * m23;
var det = a0 * b5 - a1 * b4 + a2 * b3 + a3 * b2 - a4 * b1 + a5 * b0;
if(det == 0){
alert('error');
}
var idet = 1.0 / det;
var m = mat4_create();
m[0] = (m11 * b5 - m21 * b4 + m31 * b3) * idet;
m[1] = (-m10 * b5 + m20 * b4 - m30 * b3) * idet;
m[2] = (m13 * a5 - m23 * a4 + m33 * a3) * idet;
m[3] = (-m12 * a5 + m22 * a4 - m32 * a3) * idet;
m[4] = (-m01 * b5 + m21 * b2 - m31 * b1) * idet;
m[5] = (m00 * b5 - m20 * b2 + m30 * b1) * idet;
m[6] = (-m03 * a5 + m23 * a2 - m33 * a1) * idet;
m[7] = (m02 * a5 - m22 * a2 + m32 * a1) * idet;
m[8] = (m01 * b4 - m11 * b2 + m31 * b0) * idet;
m[9] = (-m00 * b4 + m10 * b2 - m30 * b0) * idet;
m[10] = (m03 * a4 - m13 * a2 + m33 * a0) * idet;
m[11] = (-m02 * a4 + m12 * a2 - m32 * a0) * idet;
m[12] = (-m01 * b3 + m11 * b1 - m21 * b0) * idet;
m[13] = (m00 * b3 - m10 * b1 + m20 * b0) * idet;
m[14] = (-m03 * a3 + m13 * a1 - m23 * a0) * idet;
m[15] = (m02 * a3 - m12 * a1 + m22 * a0) * idet;
return m;
// http://docs.closure-library.googlecode.com/git/local_closure_goog_vec_mat4.js.source.html
}
function mat4_transpose(m1)
{
var m = mat4_create();
m[ 0] = m1[ 0]; m[ 1] = m1[ 4]; m[ 2] = m1[ 8]; m[ 3] = m1[12];
m[ 4] = m1[ 1]; m[ 5] = m1[ 5]; m[ 6] = m1[ 9]; m[ 7] = m1[13];
m[ 8] = m1[ 2]; m[ 9] = m1[ 6]; m[10] = m1[10]; m[11] = m1[14];
m[12] = m1[ 3]; m[13] = m1[ 7]; m[14] = m1[11]; m[15] = m1[15];
return m;
}
function mat4_identity()
{
var m = mat4_create();
m[ 0] = 1; m[ 1] = 0; m[ 2] = 0; m[ 3] = 0;
m[ 4] = 0; m[ 5] = 1; m[ 6] = 0; m[ 7] = 0;
m[ 8] = 0; m[ 9] = 0; m[10] = 1; m[11] = 0;
m[12] = 0; m[13] = 0; m[14] = 0; m[15] = 1;
return m;
}
function mat4_translate(a, b, c)
{
var m = mat4_create();
m[ 0] = 1; m[ 1] = 0; m[ 2] = 0; m[ 3] = 0;
m[ 4] = 0; m[ 5] = 1; m[ 6] = 0; m[ 7] = 0;
m[ 8] = 0; m[ 9] = 0; m[10] = 1; m[11] = 0;
m[12] = a; m[13] = b; m[14] = c; m[15] = 1;
return m;
}
function mat4_rotate_x(t)
{
var m = mat4_create();
m[ 0] = 1; m[ 1] = 0; m[ 2] = 0; m[ 3] = 0;
m[ 4] = 0; m[ 5] = Math.cos(t); m[ 6] = -Math.sin(t); m[ 7] = 0;
m[ 8] = 0; m[ 9] = Math.sin(t); m[10] = Math.cos(t); m[11] = 0;
m[12] = 0; m[13] = 0; m[14] = 0; m[15] = 1;
return m;
}
function mat4_rotate_y(t)
{
var m = mat4_create();
m[ 0] = Math.cos(t); m[ 1] = 0; m[ 2] = Math.sin(t); m[ 3] = 0;
m[ 4] = 0; m[ 5] = 1; m[ 6] = 0; m[ 7] = 0;
m[ 8] = -Math.sin(t); m[ 9] = 0; m[10] = Math.cos(t); m[11] = 0;
m[12] = 0; m[13] = 0; m[14] = 0; m[15] = 1;
return m;
}
function mat4_rotate_z(t)
{
var m = mat4_create();
m[ 0] = Math.cos(t); m[ 1] = -Math.sin(t); m[ 2] = 0; m[ 3] = 0;
m[ 4] = Math.sin(t); m[ 5] = Math.cos(t); m[ 6] = 0; m[ 7] = 0;
m[ 8] = 0; m[ 9] = 0; m[10] = 1; m[11] = 0;
m[12] = 0; m[13] = 0; m[14] = 0; m[15] = 1;
return m;
}
function mat4_multiply(m1, m2)
{
var m = mat4_create();
m[0] = m1[0]*m2[0] + m1[1]*m2[4] + m1[2]*m2[8] + m1[3]*m2[6];
m[1] = m1[0]*m2[1] + m1[1]*m2[5] + m1[2]*m2[9] + m1[3]*m2[13];
m[2] = m1[0]*m2[2] + m1[1]*m2[6] + m1[2]*m2[10] + m1[3]*m2[14];
m[3] = m1[0]*m2[3] + m1[1]*m2[7] + m1[2]*m2[11] + m1[3]*m2[15];
m[4] = m1[4]*m2[0] + m1[5]*m2[4] + m1[6]*m2[8] + m1[7]*m2[12];
m[5] = m1[4]*m2[1] + m1[5]*m2[5] + m1[6]*m2[9] + m1[7]*m2[13];
m[6] = m1[4]*m2[2] + m1[5]*m2[6] + m1[6]*m2[10] + m1[7]*m2[14];
m[7] = m1[4]*m2[3] + m1[5]*m2[7] + m1[6]*m2[11] + m1[7]*m2[15];
m[8] = m1[8]*m2[0] + m1[9]*m2[4] + m1[10]*m2[8] + m1[11]*m2[12];
m[9] = m1[8]*m2[1] + m1[9]*m2[5] + m1[10]*m2[9] + m1[11]*m2[13];
m[10] = m1[8]*m2[2] + m1[9]*m2[6] + m1[10]*m2[10] + m1[11]*m2[14];
m[11] = m1[8]*m2[3] + m1[9]*m2[7] + m1[10]*m2[11] + m1[11]*m2[15];
m[12] = m1[12]*m2[0] + m1[13]*m2[4] + m1[14]*m2[8] + m1[15]*m2[12];
m[13] = m1[12]*m2[1] + m1[13]*m2[5] + m1[14]*m2[9] + m1[15]*m2[13];
m[14] = m1[12]*m2[2] + m1[13]*m2[6] + m1[14]*m2[10] + m1[15]*m2[14];
m[15] = m1[12]*m2[3] + m1[13]*m2[7] + m1[14]*m2[11] + m1[15]*m2[15];
return m;
}
function vec4_create(s)
{
v = new Float32Array(4);
v[0] = 0;
v[1] = 0;
v[2] = 0;
v[3] = 0;
if(s){
v.set(s);
}
return v;
}
function vec4_translate(v, a, b, c)
{
v[0] += a;
v[1] += b;
v[2] += c;
}
function vec4_rotate_x(v, t)
{
var y = v[1], z = v[2];
v[1] = y*Math.cos(t) - z*Math.sin(t);
v[2] = y*Math.sin(t) + z*Math.cos(t);
}
function vec4_rotate_y(v, t)
{
var x = v[0], z = v[2];
v[0] = x*Math.cos(t) + z*Math.sin(t);
v[2] = -x*Math.sin(t) + z*Math.cos(t);
}
function vec4_rotate_z(v, t)
{
var x = v[0], y = v[1];
v[0] = x*Math.cos(t) - y*Math.sin(t);
v[1] = x*Math.sin(t) + y*Math.cos(t);
}mat4_translateが平行移動行列、mat4_rotate_?が回転行列を作成する関数です。また、行列の積はmat4_multiplyで計算します。
図形の変形を複数回適用する場合は行列を使うと便利ですが、別にわざわざ行列を作成しなくても変換後の座標を計算することはできます。(例えば、平行移動であれば、単に成分ごとの和を計算するだけです。)ここでは詳しく書けませんでしたが、行列を作らずに直接変換後の座標を計算する関数がvec4_translateとvec4_rotate_?になります。
| mat4_create() | 4×4行列を生成 |
| mat4_identity() | 4×4の単位行列を生成 |
| mat4_translate(a, b, c) | x軸方向にa、y軸方向にb、z軸方向にcだけ移動する平行移動行列を生成 |
| mat4_rotate_x(t) | x軸のまわりにtだけ回転する回転行列を生成 |
| mat4_rotate_y(t) | y軸のまわりにtだけ回転する回転行列を生成 |
| mat4_rotate_z(t) | z軸のまわりにtだけ回転する回転行列を生成 |
| mat4_multiply(m1, m2) | 行列の積m1×m2を計算 |
| vec4_create(s) | 4次元ベクトルを生成、sがある場合はsで初期化 |
| vec4_translate(v, a, b, c) | vをx軸方向にa、y軸方向にb、z軸方向にcだけ平行移動 |
| vec4_rotate_x(v, t) | vをx軸のまわりにtだけ回転 |
| vec4_rotate_y(v, t) | vをy軸のまわりにtだけ回転 |
| vec4_rotate_z(v, t) | vをz軸のまわりにtだけ回転 |
※この行列演算ライブラリは勉強用のサンプルです。実際に何かを作る際は他のライブラリを使うことをおすすめします。


